
In a previous document I've explained how to use the CAPM model to create naive ranking for pokemon. Even though the approach had some logic to it, I wanted to explore if a naive probibalistic implementation of trueskill could do the job as well. This document contains a python implementation my naive approach as well as an application to a pokemon dataset. The first part will explain how it is made and tested. The second part will analyse the ranking of all 750 pokemon.
Starting Data
Before writing any application code, it seems sensible to first think about how to test if the code works. It would be a good idea to simulate some random players with predetermined skill levels such that we can test if our ranking algorithm can at least rank simulated data well enough. The code below generates this data.
import uuid
import numpy as np
import pandas as pd
import json
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn; seaborn.set()
SIZE_ARR = 100
def sim(p1, p2, entropy = 1):
'''
Given two players (tuples: <name, skill>) simulate
a game between them. Returns (winner-name, loser-name)
'''
r = np.random.randint(-entropy, entropy + 1)
if p1[1] + r > p2[1]:
return p1[0], p2[0]
else:
return p2[0], p1[0]
def gen_data(n_users = 20, n_games = 100, entropy = 1):
'''
Generate a lot of games and outputs a list of user tuples
(<name>, <skill>)as well as a list of games played.
'''
data = []
users = [(str(uuid.uuid4())[:6], i) for i in range(n_users)]
for in range(n_games):
i, j = np.random.choice(range(len(users)), 2)
u1, u2 = users[i], users[j]
data.append(sim(u1, u2, entropy))
return users, pd.DataFrame(data, columns = ['winner', 'loser'])
Code that does the math
We'll now concern ourselves with writing code that updates a system of beliefs. The belief will be captured in a numpy array and can be interpreted as a histogram of likelihood values for a certain level of skill. The algorithm is explained in the previous blogpost as well but schematically, this is what the belief update looks like;
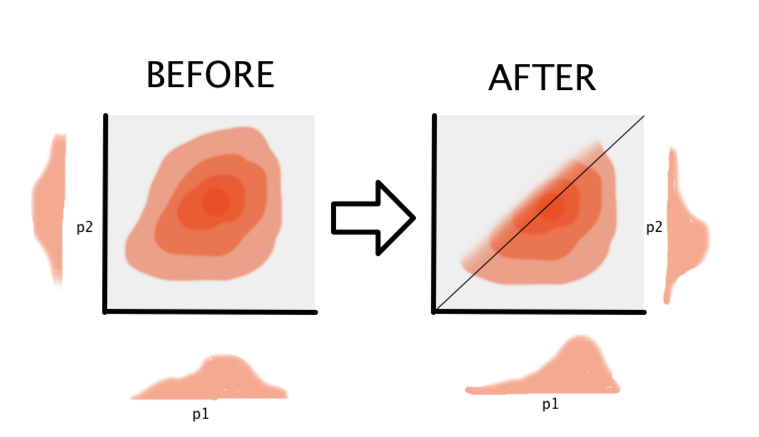
We start out with two arrays of prior skill beliefs for player 1 and player 2. We then combine them in a two dimensional density. This is our prior belief of the skill levels of the two players. Once a player wins, we can update this belief. One player has a lower skill level. To translate this to our belief system, we cut away all likelihood in the triangle of the losing player. Then we marginalise our belief back to the two players. By repeating this for all the games, we hope to achieve a belief of skill that can be updated in real time.
Towards Code
Next we'll define all the functions that do the ranking. These functions are meant to be minimal, as we only want to check if this algorithm can work. It makes sense to think about what our app code might look like and to think about how to test individual components before writing the code though. I'm not particularily religious about testing but I do see some value for writing a test before writing code here. We're going to be munging with numpy matrices and typos in indices will be unforgiving.
p1 = np.array([1.,2.,3.])
p2 = np.array([3.,2.,1.])
p3 = np.array([1.,1.,1.])
mat1 = gen_prior(p1, p2)
mat2 = gen_prior(p2, p1)
mat3 = gen_prior(p3, p3)
m1, m2 = gen_marginals(mat1)
m3, m4 = gen_marginals(mat2)
np1, np2 = gen_marginals(cut_matrix(mat1))
assert all(m1 == m2[::-1]) #marginals should still be same shape
assert all(m3 == m4[::-1]) #marginals should still be same shape
assert np.sum(mat1) == np.sum(mat2) #matrices should have equal values
assert np.sum(mat3) == 9 #all ones should sum to 9
assert all(np1 == np2[::-1]) #marginals should still be same shape
With these tests in place, I could move on to the code.
def get_player_stats(name):
'''
Check if a player exists in the dictionary. If not, add it.
Then returns the player belief.
'''
if name not in d.keys():
d[name] = np.ones(SIZE_ARR)/np.sum(np.ones(SIZE_ARR))
return d[name]
def gen_prior(arr1, arr2):
'''
Combines two arrays into a matrix.
'''
return np.matrix(arr1).T np.matrix(arr2)
def cut_matrix(mat):
'''
Cuts the matrix according to likelihood update rule.
Also applies normalisation
'''
posterior = np.triu(mat) + 0.000001
posterior = posterior/np.sum(posterior)
return posterior
def gen_marginals(posterior_mat):
'''
From a cut matrix, generate the appropriate marginals back
'''
winner = np.squeeze(np.asarray(np.sum(posterior_mat, 0)))
loser = np.squeeze(np.asarray(np.sum(posterior_mat, 1)))
return winner, loser
def update(winner, loser):
'''
Given a winner and user, update our state.
'''
winner_arr = get_player_stats(winner)
loser_arr = get_player_stats(loser)
prior_mat = gen_prior(loser_arr, winner_arr)
posterior_mat = cut_matrix(prior_mat)
new_winner, new_loser = gen_marginals(posterior_mat)
d[loser] = new_loser
d[winner] = new_winner
I wrote the code and the tests passed. For now this is enough. Before running this code against the pokemon dataset, let us first run it against some simulated data.
Running the code a few times.
First let's define a few functions that automate plotting.
def plot_scores(plot_idx):
plt.subplot(plot_idx)
plt.scatter(
np.arange(len(users)),
[np.mean(d[usr[0]] np.arange(SIZE_ARR)) for usr in users])
def plot_dist(plot_idx):
plt.subplot(plot_idx)
for usr in users:
plt.plot(np.arange(SIZE_ARR), d[usr[0]], alpha = 0.5)
Next we'll run some experiments.
Simulate n_players = 100, n_games = 400, entropy = 1
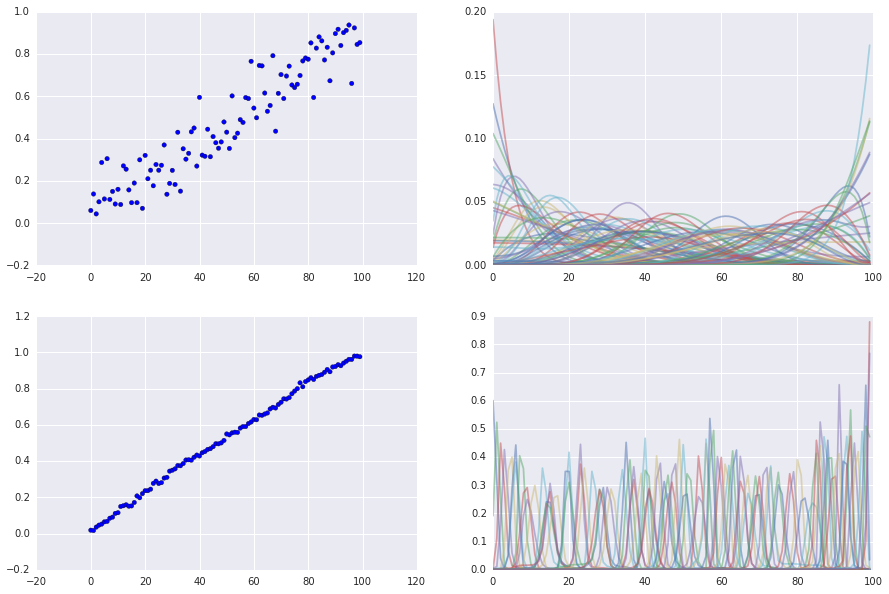
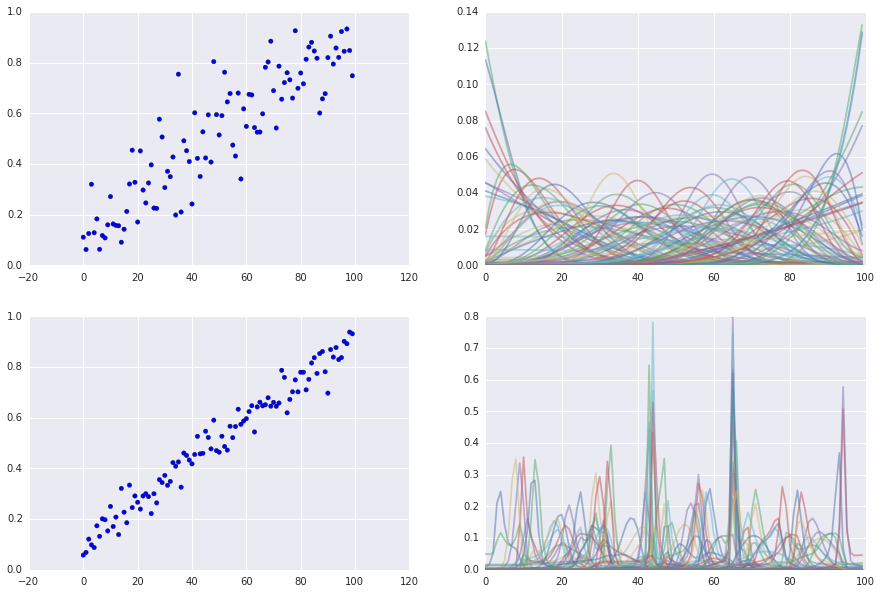
Simulate n_players = 100, n_games = 400/10000, entropy = 15
Simulate n_players = 100, n_games = 400/10000, entropy = 50
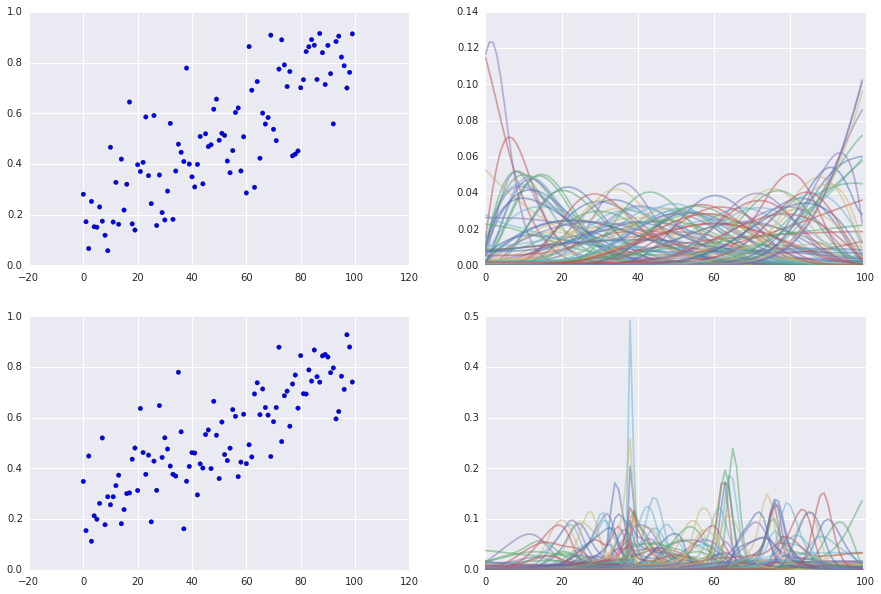
There's still some room for improvement to this system to make the convergence better, but it seems well enough for my purposes. I want to use this metric to rank pokemon so if I need to simulate some more outcomes between two pokemon then I won't mind. For more real-time purposes, the following tweaks seem to be important;
- New matches are allocated randomly, which is suboptimal from a learning perspective. If you want to fine tune the top 10 players it makes sense to have them play against eachother if you are unsure who is number 1. If instead you'd have one of these players compete against somebody mediocre you can predict the game outcome before it even started. This means you would not learn anything from that game.
- I am using buckets to simulate a distribution for a player. It may be better to use Beta distributions instead and save it's parameters. This would make the blogpost harder to read for more novice readers which is the main reason of not doing it, but this should improve the stability and remove the need for the hard coded smoothing parameter in the cut_matrix function.
For the pokemon dataset I only have one concern; the effect of rock paper scissors.
Pokemon Data
I took the liberty of preparing a dataset. It's easy to do yourself with a bit of python and this project. I'll use the formula from my previous post here again to create a function that can simulate the outcome of a pokemon battle. It will be based on the number of turns that one pokemon can outlast the other.
$$ T_{ij} = \frac{HP_i}{DMG_{ji}} $$
where $T_{ij}$ is the number of turns the pokemon $i$ would be able to survive the opponent $j$ if it were to be attacked indefinately,
$HP_i$ is the amount of hitpoints that pokemon $i$ has and $DMG_{ji}$ is the amount of damage a basic attack pokemon $j$ would deal to pokekom $i$. This damage is defined via:
$$ DMG_{ji} = \frac{2L_j + 10}{250} \times \frac{A_j}{D_i} \times w_{ji} $$
The situation will very much assume some core aspects of the game away. The hope is that my making this assumption we'll still leave much of the actual pokemon game intact. For ease of use, you can read the datasets from my hosted blog.
poke_df = pd.read_csv("http://koaning.io/theme/data/full_pokemon.csv")
weak_df = pd.read_csv("http://koaning.io/theme/data/pokemon_weakness.csv")
def weakness_weight(types_j, types_i):
"""
Returns w_{ji}
"""
res = 1.
possible_types = [t for t in weak_df['type']]
for i in filter(lambda t: t in possible_types, types_i):
for j in filter(lambda t: t in possible_types, types_j):
res = float(weak_df[weak_df['type'] == j][i])
return res
def calc_tij(poke_i, poke_j):
"""
Calculate the number of turns one pokemon would outlast the other.
"""
poke_row_i, poke_row_j = poke_df[poke_df['name'] == poke_i].iloc[0], poke_df[poke_df['name'] == poke_j].iloc[0]
dmg_ji = (200. + 10)/250
dmg_ji = float(poke_row_j['attack'])/float(poke_row_i['defence'])
dmg_ji *= weakness_weight(eval(poke_row_j['type']), eval(poke_row_i['type']))
return poke_row_i['hp']/dmg_ji
def sim_poke_battle(poke_i, poke_j):
"""
Simulate the outcome between two pokemon. Output: winner_name, loser_name.
"""
if calc_tij(poke_i, poke_j) > calc_tij(poke_j, poke_i):
return poke_i, poke_j
return poke_j, poke_i
I ran some of the code, and the posterior output looked like this:
The maximum likelihood then gives an insight for the best/worst pokemon.
name mle name mle
128 Magikarp 0.011007 142 Snorlax 0.877423
112 Chansey 0.013735 248 Lugia 0.882689
348 Feebas 0.015845 487 Cresselia 0.883819
171 Pichu 0.019108 66 Machoke 0.887577
291 Shedinja 0.020473 713 Avalugg 0.890049
439 Happiny 0.026763 380 Latios 0.893087
241 Blissey 0.037009 148 Dragonite 0.895297
172 Cleffa 0.042802 611 Haxorus 0.895832
234 Smeargle 0.048575 290 Ninjask 0.897319
49 Diglett 0.054010 388 Torterra 0.902103
400 Kricketot 0.057252 717 Yveltal 0.904122
297 Azurill 0.058177 646 Kyurem 0.914460
235 Tyrogue 0.060337 485 Regigigas 0.916059
659 Bunnelby 0.060847 305 Aggron 0.916220
62 Abra 0.064720 597 Ferrothorn 0.916377
173 Igglybuff 0.068975 425 Drifblim 0.917240
190 Sunkern 0.071101 644 Zekrom 0.919065
279 Ralts 0.081876 537 Throh 0.921175
160 Sentret 0.082374 482 Dialga 0.928502
51 Meowth 0.083082 149 Mewtwo 0.951472
174 Togepi 0.087797 483 Palkia 0.953823
581 Vanillite 0.091351 288 Slaking 0.956629
212 Shuckle 0.095570 375 Metagross 0.957383
18 Rattata 0.100470 492 Arceus 0.957729
330 Cacnea 0.100798 716 Xerneas 0.960467
Conclusion
I have run this algorithm a few times and it seems doesn't seem to converge very consistently. It does some things very well; the fact that magicarp is generally performing poorly is good news. I've also noticed Mew/Mewtwo in the higher skilled area. I'm still concerned that this algorithm fails to grasp the rock/paper scissors element that is in the game. But the fact that I am assuming that every pokemon is fighting with only basic attacks also does not help.
As a final push one might consider making an ensemble of these pokemon rankings to see if the convergence can be make to go faster. Another tweak to consider is to have the matching of these pokemon not be random during the learning. I like the results of the exercise, but it seems that we are not done with ranking pokemon.