Rstudio has a nice Rcpp support so you can write very performant C++ code for R. So I thought I'd give it a spin to test out some benchmarks.
Estimating Pi
I defined three functions in C++ that would be exported to R to be benchmarked.
#include <Rcpp.h>
#include <random>
using namespace Rcpp;
// [[Rcpp::export]]
NumericVector runifC(int n, double min=0, double max=1, int seed = 1) {
NumericVector out(n);
srand(seed);
for(int i = 0; i < n; ++i) {
out[i] = min + ((double) std::rand() / (RAND_MAX)) * (max - min);
}
return out;
}
// [[Rcpp::export]]
double calcpi(int n){
double inside = 0;
srand(1);
for(int i = 0; i < n; ++i){
double x = ((double) rand() / (RAND_MAX));
double y = ((double) rand() / (RAND_MAX));
if( x*x + y*y < 1.0 ){
inside = inside + 1;
}
}
return(4 * inside / n);
}
// [[Rcpp::export]]
double piSugar(const int N) {
NumericVector x = runif(N);
NumericVector y = runif(N);
NumericVector d = sqrt(x*x + y*y);
return 4.0 * sum(d < 1.0) / N;
}
I then used the following R code to run the benchmarks.
library(microbenchmark)
calcpiR = function(n){
inside = 0;
for(i in 1:n) {
randx = runif(1)
randy = runif(1)
if( runif(1)^2 + runif(1)^2 < 1 ){
inside = inside + 1;
}
}
return(inside/n*4);
}
microbenchmark(
'R pi func' = calcpiR(1000),
'R pi vector'= sum(runif(10000)^2+runif(10000)^2 < 1)*4/10000,
'C pi rsugar'= piSugar(10000),
'C pi pure' = calcpi(10000)
)
All the functions gave similar output near the true value of pi as you would expect but the calculation time differs drastically.
expr min lq mean median uq max neval
R pi func 10327.084 11116.0940 17407.7221 11578.8145 12922.3245 137028.958 100
R pi vector 594.415 615.1175 742.2290 635.5280 737.3465 1513.818 100
C pi rsugar 228.696 239.5440 318.1537 244.8380 307.3430 775.505 100
C pi pure 170.483 171.3055 182.8474 173.5915 178.2010 360.292 100
Caveat
It seems odd that a way faster implementation of the runif functions exists without it being implemented in R. There is a drawback though, that frankly, is a little scary.
Random numbers cannot actually be generated by a machine so all sorts of clever tricks are used to mimic randomness. Random number generators both in R and in C make use of a random seed. The seed tells the generator where in the giant list of random numbers to start drawing numbers from. That is why if you set the same seed that you can expect the same random numbers.
For more statistical and cryptographical purposes, you usually really care that numbers actually generated randomly. If you have two different random seeds that generate a random list each, you don't want there to be any relationship between two list of random numbers.
This is where the C++ standard implementation scares people. To show how, I've simulated some data using the standard runif function from R and the runifC C++ function that I've defined earlier.
seeds = 30
df = data.frame(seed1=as.numeric(c()), seed2=as.numeric(c()), cor=as.numeric(c()))
for(i in 1:seeds){
for(j in i:seeds){
r1 = runifC(100000,0,1,i)
r2 = runifC(100000,0,1,j)
df = rbind(df, data.frame(seed1=i, seed2=j, cor=cor(r1,r2)))
}
print(i)
}
ggplot() + geom_tile(data=df2, aes(seed1, seed2, fill=cor)) + ggtitle("c random seed correlations")
df = data.frame(seed1=as.numeric(c()), seed2=as.numeric(c()), cor=as.numeric(c()))
for(i in 1:seeds){
for(j in i:seeds){
set.seed(i)
r1 = runif(100000)
set.seed(j)
r2 = runif(100000)
df = rbind(df, data.frame(seed1=i, seed2=j, cor=cor(r1,r2)))
}
print(i)
}
ggplot() + geom_tile(data=df2, aes(seed1, seed2, fill=cor)) + ggtitle("r random seed correlations")
This script generates two correlation tileplots. I am checking the correlation between different random arrays caused by different random seeds in the two random generators.
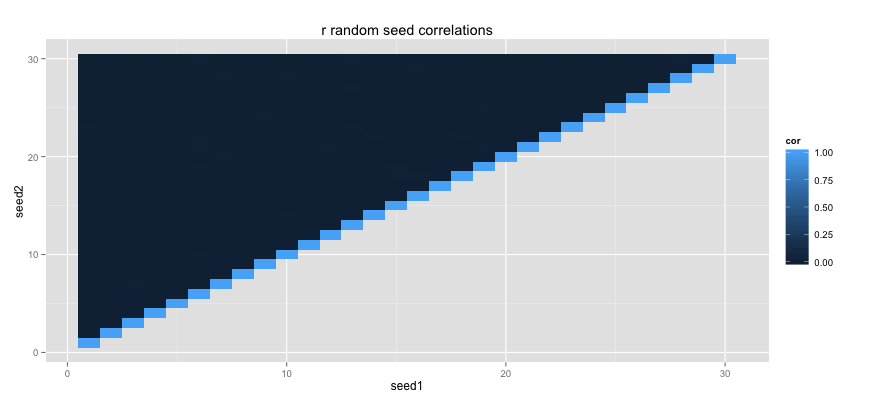
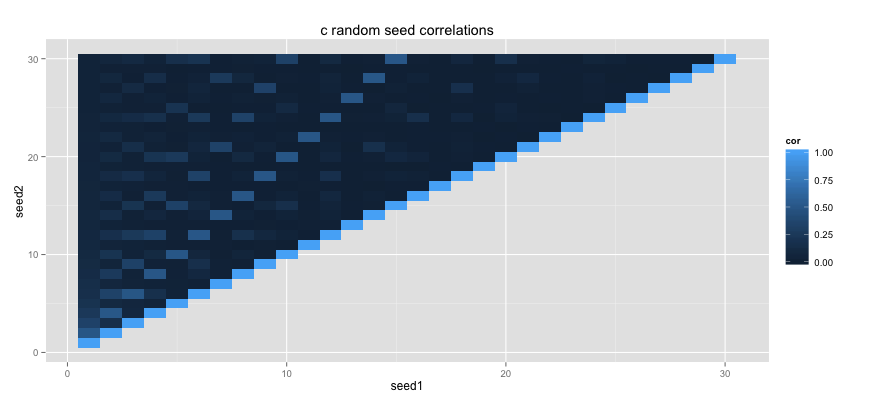
Ouch. The C++ code might run a lot faster, but the way it handles random seeds is slightly scary. It may be a whole lot safer to use the suger coated Rcpp code instead.
You should also be able to find this blog on: r-bloggers