This document contains three different ways of interpreting a linear regression based on three popular schools of data. The hope is that it may help explain the difference between three schools of thought in data science. It is written from the viewpoint from somebody in industry, not academia.
Simple Observation
In data land, it seems like there are three schools on how to do things.

Each school tends to look at data a bit differently and each school has a small tendancy of pointing out the flaws of the others. The truth is probably in the middle as the schools actually overlap quite a bit. There's some non overlapping opinion and some techniques that differ though.
Frequentists are known for hypothesis tests, p-values and significance summary statistics. Bayesians are known for sampling techniques, inference, priors and posteriors. Machine learnings come to the field with ensembler techniques, forests, support vector machines and neural networks.
It is a good thing that people have different views otherwise the world would always look the same. Different views lead to good discussions which help us understand the field of data better. What I'm less a fan of is people making claims that they are better at data simply because they're using a set of models exclusive to their school. Calling a tensorflow model instead of applying probabilistic inference does not make you the Chuck Norris among your peers in the same way that exclusively using an oven doesn't makes you a better cook.
Interestingly, all schools use linear regression but interpret at it from a different angle. So let's use that as a tangible example to show how these three schools think differently about modelling.
Where is your schools uncertainty?
If I were to look at the schools from a distance, it seems like they all adhere to this basic rule of science.
All models are wrong. Some models are useful.
They do however, seem to think differently on how to deal with uncertainty. To figure out where you are, ask yourself. When you look at your model, what are you most uncertain about?
- Are you unsure about the data and are you trying to find the best parameters to describe your model?
- Are you unsure about the model and do you accept the data to be the main truth available?
- Are you willing to ignore all uncertainties when your black box model performs very well against a lot of test sets?
There is some sense in all three approaches but they are different. Let's describe a regression task as an example to make this difference a bit more tangible.
Illustrative Example: Regression
Suppose that we have a regression task. We have some data $X$ and some variable we'd like to predict $y$. We'll assume that this dataset fits into a table and that there are $k$ columns in $X$ and $n$ rows.
Frequentist View
A frequentist would look at the regression by looking at it as if it were an hypothesis test. For every column of data we'd want to check if has a significant contribution to the model. We fit the data to the model, optimising for mean squared error (or mean absolute error) and assume some form of standard error on the data. This gives us our estimate $\hat{\beta}$, which is different from the true $\beta^*$. This difference is modelled by including a normal error.
$$ y \approx X\hat{\beta} $$ $$ y = X\beta + e $$ $$ e \sim N(0, \sigma) $$
By combining a bit of linear algebra and statistics you can use this to come to the conclusion that you can create a hypothesis test for every column $k$ in the model where the zero hypothesis is that $\beta_k$ should be zero. This test requires a T-distribution and there's a proof for it. This is why so many statistics papers have summaries like this:
Residuals:
Min 1Q Median 3Q Max
-103.95 -53.65 -13.64 40.38 230.05
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 102.645 4.674 21.961 < 2e-16 ***
Diet2 19.971 7.867 2.538 0.0114 *
Diet3 40.305 7.867 5.123 4.11e-07 ***
Diet4 32.617 7.910 4.123 4.29e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 69.33 on 574 degrees of freedom
Multiple R-squared: 0.05348, Adjusted R-squared: 0.04853
F-statistic: 10.81 on 3 and 574 DF, p-value: 6.433e-07
There's a lot of assumptions involved don't feel obvious to me but can hold for a lot of cases. Assuming normality is a thing but assuming that all columns are independant is a big one. Frequentists are usually aware of this which is why after modelling the regression with good columns one usually runs hypothesis tests on the assumptions that went into the model. This is why you'll notice quite a few statistics listed in the regression output.
Bayesian View
A bayesian would look at the task and immediately write down;
$$ p(\theta | D) = \frac{p(D | \theta)p(\theta)}{p(D)} \propto p(D | \theta)p(\theta) = p(\theta) \Pi_i p(x_i| \theta)$$
Here, $\theta$ are the parameters of the model that need to be learned from the available data $D$. By applying bayes rule the bayesian would argue that this is proportional to a likelihood $p(D | \theta)$ and a prior $p(\theta)$. In linear regression $\theta = (\beta, \sigma$).
The bayesian would not be interested in maximum likely value of $\theta$. In fact, the bayesian would not even consider $\hat{\theta}$ that much of a special citizen. The goal is to derive the distribution of $p(\theta | D)$ instead because this holds much more information.
The downside is that this task is harder from a maths perspective because $p(\theta | D)$ is a $(k + 1)$-dimensional probability distribution. Luckily, because you can model $\Pi_i p(x_i| \beta)$ you can use sampling techniques like MCMC or variational inference to infer what $p(\beta | D)$ might be. A helpful realisation is that you'll only need to figure out this bit yourself;
$$ p(x_i| \beta, \sigma) \sim N(X\beta, \sigma) $$
This defines the likelihood that given certain model parameters you'll witness a point $x_i$ in your data. The derivation of this is somewhat obvious for a linear regression, but less obvious for other models.
A benefit of looking at it from this way is that you are able to apply inference on a stream of data instead of just a batch of data. You can learn quite a bit from small datasets and you usually get a good opportunity to learn from the world instead of merely trying to predict it.
People sometimes critique the bayesian approach because you need to supply it with a prior $p(\theta)$. Bayesian usually respond by saying that all models require some assumptions and that it is a sensible thing to put domain knowledge into a model when applicable. I personally find the choice of model part $p(x_i | \beta)$ to be the biggest assumption in the entire model to such an extend that it seems worthless to even worry about the prior $p(\theta)$.
Machine Learning View

The machine learning specialist won't mind to view the problem as a black box. A typical approach would go as far as not generting one model but many. After all, training many models on subsets of the data (both rows and columns) might give better performance in the test set. The output of these regressions may then potentially be used as input for ever more regressions. One of these regressions might actually be a tree model in disguise, we can apply many tricks to prevent overfitting (L1/L2 regularisation) and we may even go a bit crazy in terms of feature engineering. We might even do something fancy by keeping track of all the mistakes that we make and try to focus on those as we're training (boosting, confusion matrix reweighting).
Typically the machine learning specialist would ignore any statistical properties of the regression. Instead, one would run many versions of this algorithm many many times on random subsets of the data by splitting it up into training and test sets. One would then accept the model that performs best in the test set as the best model and this would be a candidate for production.
Conclusion
When looking at the regression example I would argue that these three approaches overlap more than they differ but I hope that the explanation does show the subtle differences in the three schools. Depending on your domain you may have a preference to the modelling method. In the end, the only thing that matters is that you solve problems. The rest is just theoretical banther.
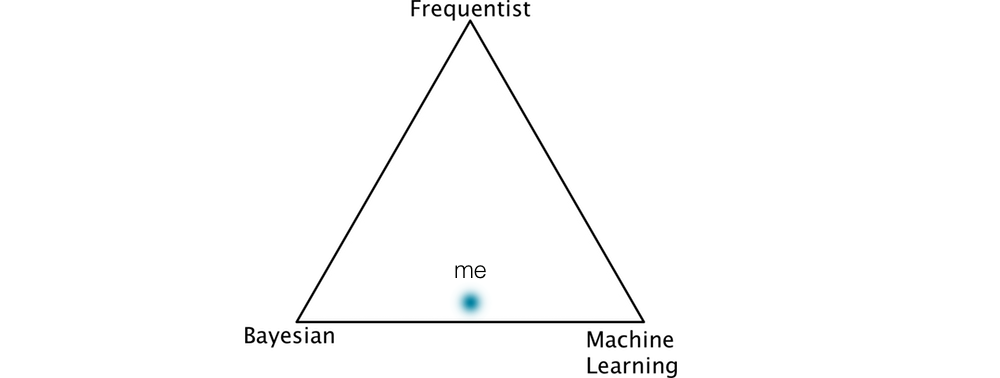
If I have to place myself on the triangle, I'd be at the bottom somewhere between bayes and ML. The only reason for being there is that I'm able to solve the most problems that way and the assumptions frequentist sometimes gets in my way (link to rather impolite rant). I feel comfortable near the edge of the triangle but there is danger in being stuck in a single corner. You may an epic ensembling machine learning wizard, if that is all you can do then you're missing out.
Cool things happen when you combine methods from different schools. Many recent NIPS papers dicuss bayesian interpretation of neural networks; variational inference, sampling techniques and networks as generative approximators are all trends that combine knowledge from both schools. It just goes to show that if you try to learn from another school, you might just be able to solve different problems.
Or in other words;
Never let your school get in the way of your education.